八皇后问题与Las Vegas算法的结合
八皇后问题一直是回溯算法的经典问题。最近在上概率算法,涉及到八皇后问题与Las Vegas算法的结合,花了两天时间写代码,调bug,故特此写下这篇博客以做总结。
传统的回溯法
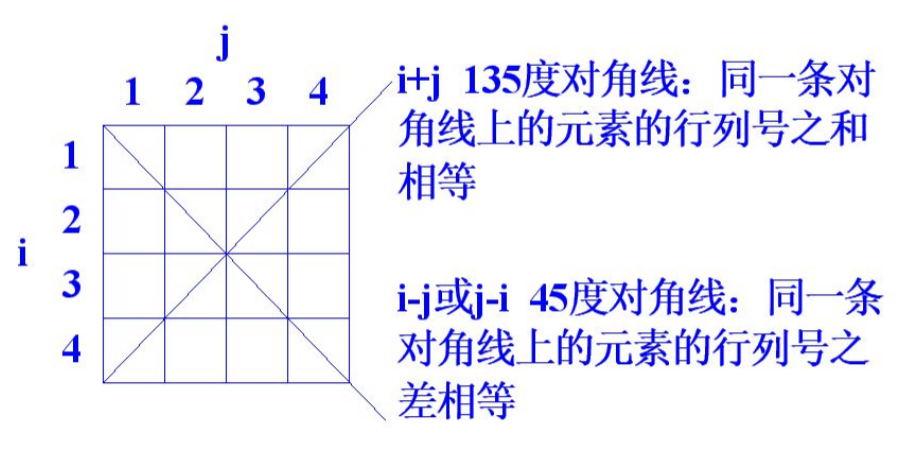
- 伪代码

- 代码
1 |
|
Las Vegas算法
- Las Vegas算法介绍


- 伪代码


- 代码
1 |
|
问题及改进
- 概况


- 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
using namespace std;
int trycol[100];
bool isPositionOpen(int x, int y, vector<int> col, vector<int> diag45, vector<int> diag135)
{
int tem;
//判断列号
for(tem = 0; tem < col.size(); tem++){
if(col[tem] == y)
return false;
}
//判断45度对角线 45度对角线利用x - y x为行号,y为列号
for(tem = 0; tem < diag45.size(); tem++){
if(diag45[tem] == x-y)
return false;
}
//判断135度对角线
for(tem = 0; tem < diag135.size(); tem++){
if(diag135[tem] == x+y)
return false;
}
return true;
}
void backtrace (int k, vector<int> col, vector<int> diag45, vector<int> diag135, bool &success)
{
stack<int> colStack;
int i = k, j = 1, tem;
bool isOpenFind;
while(i <= QueenNumber){
isOpenFind = false;
//检查当前行i:从当前列j起向后逐列试探,寻找安全序号
while(j <= QueenNumber){
if(isPositionOpen(i, j, col, diag45, diag135)){
isOpenFind = true;
col.push_back(j);
diag45.push_back(i-j);
diag135.push_back(i+j);
break;
}
j++;
}
//找到安全列号
if(isOpenFind){
colStack.push(j);
i++;
j = 1;
}
//未找到安全列号
else{
if(colStack.empty()){
success = false;
return;
}
j = colStack.top();
colStack.pop();
i--;
for (vector<int>::iterator iter = col.begin(); iter != col.end(); ++iter){
if(*iter == j){
col.erase(iter);
break;
}
}
for (vector<int>::iterator iter = diag45.begin(); iter != diag45.end(); ++iter){
if(*iter == i-j){
diag45.erase(iter);
break;
}
}
for (vector<int>::iterator iter = diag135.begin(); iter != diag135.end(); ++iter){
if(*iter == i+j){
diag135.erase(iter);
break;
}
}
j++;
}
}
success = true;
for(tem=QueenNumber; tem>=k; tem--){
trycol[tem] = colStack.top();
colStack.pop();
}
}
void QueenLV(bool &success)
{
vector<int> col, diag45, diag135;
col.clear();
diag45.clear();
diag135.clear();
int k = 0, nb, i, j;
random_device rd;
mt19937 gen(rd());
do{
nb = 0;
for(i = 1; i <= QueenNumber; i++){
if(isPositionOpen(k+1, i, col, diag45, diag135)){
nb++;
uniform_int_distribution<> dis(1, nb);
if(dis(gen) == 1){
j = i;
}
}
}
if(nb > 0){
k++;
trycol[k] = j;
col.push_back(j);
diag45.push_back(k-j);
diag135.push_back(k+j);
}
}while(nb !=0 && k != stepVegas);
if(nb == 0){
success = false;
}
else{
backtrace(stepVegas+1, col, diag45, diag135, success);
}
}
int main()
{
bool success;
do{
QueenLV(success);
}while(!success);
if(success){
for(int i=1; i<= QueenNumber; i++){
cout<<trycol[i]<<endl;
}
}
else{
cout<<"hello world!\n"<<endl;
}
getchar();
return 0;
}
总结
Las Vegas算法与回溯法的结合往往能够提高程序的运行效率。Las Vegas算法虽然为随机算法,但是相较于确定性算法,却提高了程序的效率,这是一个值得借鉴的地方。以前接触的往往都是确定性算法,在以后的编码过程中,可以考虑加入随机算法,也许会获得意想不到的结果。