数据结构:树的归纳总结
最近,因为要准备找工作,所以本文特意总结归纳一下数据结构中重要的一块:树。
二叉查找树
二叉查找树(BST:Binary Search Tree)是一种特殊的二叉树,它改善了二叉树节点查找的效率。二叉查找树有以下性质:
对于任意一个节点 n,
- 其左子树(left subtree)下的每个后代节点(descendant node)的值都小于节点 n 的值;
- 其右子树(right subtree)下的每个后代节点的值都大于节点 n 的值。
所谓节点 n 的子树,可以将其看作是以节点 n 为根节点的树。子树的所有节点都是节点 n 的后代,而子树的根则是节点 n 本身。
BST的查找、插入、删除操作的运行时间与BST的拓扑结构有关,最佳情况是O(log n),而最坏情况是 O(n)。
AVL树
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
引入平衡二叉树的目的是为了提高二叉查找树的搜索的效率,减少树的平均搜索长度。
红黑树
红黑树是一种自平衡二叉查找树,典型的用途是实现关联数组。
红黑树的性质:
- 节点是红色或黑色
- 根是黑色
- 所有叶子都是黑色
- 每个红色节点必须有两个黑色的子节点(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点
红黑树相对于AVL树来说,牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,性能整体来说要优于AVL树。
Trie树
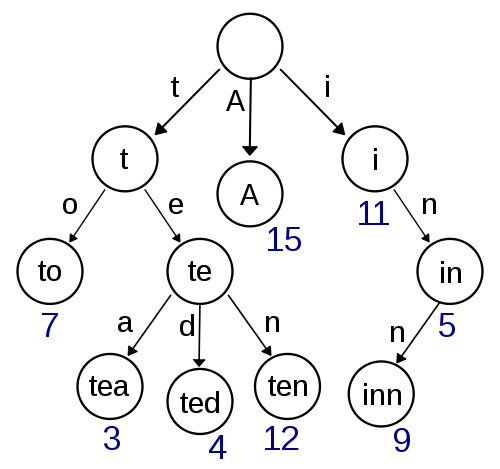
在计算机科学中,Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
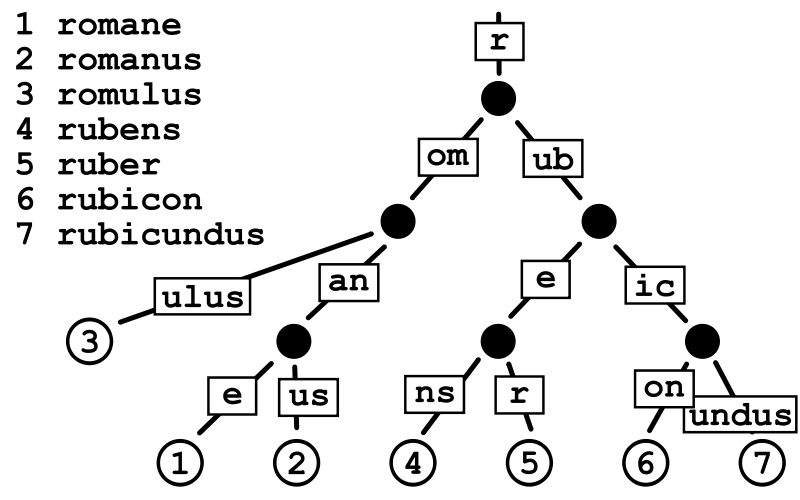
基数树(Radix Tree)
基数树,或称压缩前缀树,是一种更节省空间的Trie。对于基数树的每个节点,如果该节点是唯一的子树的话,就和父节点合并。
在Linux内核中,一个address_space对象对应一个基树。
B树与B+树
详情请从参考B树和B+树的定义以及应用。
对于在内存中的查找结构而言,红黑树的效率已经非常好了。但是如果是数据量非常大的查找呢?将这些数据全部放入内存组织成红黑树结构显然是不实际的。实际上,像OS中的文件目录存储,数据库中的文件索引结构的存储…. 都不可能在内存中建立查找结构,必须在磁盘中建立好这个结构。那么在这个背景下,红黑树显然不是一种好的选择。
在磁盘中组织查找结构,从任何一个结点指向其他结点都有可能读取一次磁盘数据,再将数据写入内存进行比较。大家都知道,频繁的磁盘IO操作,效率是很低下的(机械运动比电子运动要慢不知道多少)。显而易见,所有的二叉树的查找结构在磁盘中都是低效的。因此,B树很好的解决了这一个问题。
参考资料: